casos de factorización 2
Excelente día para todos , ahora anexo los casos 5, 6, 7 de factorización, espero les sea de ayuda en sus estudios para reforzar sus conocimientos de álgebra.
Quinto caso: Trinomio cuadrado perfecto por
adición y sustracción
— Existe
una manera de lograr trinomios cuadrados perfectos a partir de binomios si
simplemente les sumamos y restamos el término que le haga falta.
— Si
tenemos un binomio cuyos dos factores tengan raíces cuadradas se siguen los
siguientes pasos para la creación de un trinomio cuadrado perfecto:
◦ Se
les extrae la raíz cuadrada a los dos términos.
◦ Se
encuentra el doble producto de estas raíces.
◦ Este
doble producto se suma y se resta a los dos términos que son cuadrados
perfectos.
— Ejemplo:
— Si
tenemos un binomio de la forma x2 + bx hace falta completarlo con el cuadrado
de la mitad del coeficiente de la raíz del termino de la derecha.
— Ejemplo:
Sexto caso: Trinomio de la forma X^2+BX+C
— Este
tipo de trinomio tiene las siguientes características:
— Tienen
un término positivo elevado al cuadrado y con
Coeficiente 1
().
— Posee
un término que tiene la misma letra que el termino anterior pero elevada a 1
(bx) (puede ser negativo o positivo).
— Tienen
un término independiente de la letra que aparece en los otros dos (+ o -).
— Reglas
para factorizar un trinomio de esta forma:
— Se
descompone el trinomio en dos factores binomios cuyo primer término será la
raíz cuadrada del término.
— El
signo del primer binomio será el mismo signo que tenga el término “bx”, el signo
del segundo binomio será igual a la multiplicación de los signos de “bx” y de
“c”.
— Si
los dos factores tienen signos iguales entonces se buscan dos números
cuya suma sea igual que el valor absoluto del factor “b” de “bx”, y cuyo
producto sea igual al valor absoluto del factor “c”, estos números son los
segundos términos de los factores binomios.
— Si
los dos factores tienen signos diferentes entonces se buscan dos
números cuya diferencia sea igual que el valor absoluto del factor “b” de “bx”,
y cuyo producto sea igual al valor absoluto del factor “c”, el mayor de
estos números será el segundo término del primer factor binomio, y
el menor de estos números será el segundo término del
segundo factor binomio.
Séptimo caso: Trinomio de la
forma AX^2+BX+C
— Este
tipo de trinomio se diferencia del anterior debido a que el término al cuadrado
() se encuentra precedido por un coeficiente diferente de uno (debe ser
positivo). Este se trabaja de una manera un poco diferente, la cual
detallamos a continuación:
— Multiplicamos
el coeficiente “a” del factor “a” por cada término del trinomio, dejando esta
multiplicación indicada en el término “bx” de la manera “b (ax)”, y en el término
“a” de la manera.
— Se
descompone el trinomio en dos factores binomios cuyo primer término será la
raíz cuadrada del término la que sería “ax”.
— al
producto resultante lo dividimos entre el factor “a”, con el fin de no variar
el valor del polinomio.
— El
signo del primer binomio será el mismo signo que tenga el término “bx”, el
signo del segundo binomio será igual a la multiplicación de los signos de “bx”
y de “c”.
— Se
buscaran los segundos términos de los binomios según los pasos tres y cuatro
del caso del trinomio anterior.
— Ejemplo
explicativo:
— Ejemplos:
Séptimo caso: Trinomio de la
forma AX^2+BX+C
— Este
tipo de trinomio se diferencia del anterior debido a que el término al cuadrado
() se encuentra precedido por un coeficiente diferente de uno (debe ser
positivo). Este se trabaja de una manera un poco diferente, la cual
detallamos a continuación:
— Multiplicamos
el coeficiente “a” del factor “a” por cada término del trinomio, dejando esta
multiplicación indicada en el término “bx” de la manera “b (ax)”, y en el término
“a” de la manera.
— Se
descompone el trinomio en dos factores binomios cuyo primer término será la
raíz cuadrada del término la que sería “ax”.
— al
producto resultante lo dividimos entre el factor “a”, con el fin de no variar
el valor del polinomio.
— El
signo del primer binomio será el mismo signo que tenga el término “bx”, el
signo del segundo binomio será igual a la multiplicación de los signos de “bx”
y de “c”.
— Se
buscaran los segundos términos de los binomios según los pasos tres y cuatro
del caso del trinomio anterior.
— Ejemplo
explicativo:
— Ejemplos:
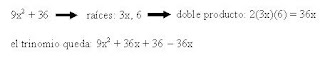






Comentarios
Publicar un comentario