Casos de Factorización
Excelente día para todos , en la entrada de hoy publicare los cuatro primeros casos de factorización con ejemplos ilustrativos espero les sea de ayuda.
PRIMER CASO:
FACTOR COMÚN
—Se dice que un polinomio tiene factor común cuando una misma cantidad,
ya sea número o letra, se encuentra en todos los términos del polinomio.
—Si en todos los términos de un polinomio figura un factor común, dicho
polinomio es igual al producto de ese factor por el polinomio que resulta al
dividir cada término por ese factor.
—Para efectuar el factor común hay que tomar en cuenta que este se realiza
tanto para los números como para las letras, y con las letras se toma la que
tenga el menor exponente de todas.
—Ejemplo:
SEGUNDO CASO: AGRUPACIÓN DE TÉRMINOS
—Se llama factor común por agrupación de términos, si los términos de un
polinomio pueden reunirse en grupos de términos con un factor común diferente
en cada grupo.
—Cuando pueden reunirse en grupos de igual número de términos se le saca
en cada uno de ellos el factor común. Si queda la misma expresión en cada uno
de los grupos entre paréntesis, se la saca este grupo como factor común,
quedando así una multiplicación de polinomios.
—Tratar desde el principio que nos queden iguales los términos de los paréntesis
nos hará mas sencillo el resolver estos problemas.
—Ejemplo:
—2ax + 2bx - ay + 5a - by + 5b
—Agrupo los términos que tienen un factor común:
(2ax - ay + 5a ) + ( 2bx - by + 5b )
—Saco el factor común de cada grupo:
a ( 2x - y +
5 ) + b (2x - y + 5 )
—Como las expresiones encerradas entre paréntesis son iguales se tiene:
( 2x -y +5
)(a + b)
—Que es nuestra respuesta.
TERCER CASO: TRINOMIO CUADRADO PERFECTO
—Se llama trinomio cuadrado perfecto al trinomio
(polinomio de tres términos) tal que, dos de sus términos son cuadrados
perfectos y el otro término es el doble producto de las bases de esos
cuadrados.
—En el trinomio cuadrado perfecto los términos cuadrados son siempre
positivos, en cambio el término del doble producto puede ser negativo; en este
caso debe ser negativo uno de los términos del binomio cuyo cuadrado es el
trinomio dado.
—Regla para conocer si un trinomio es cuadrado perfecto.
Un trinomio ordenado con relación a una letra
es cuadrado perfecto cuando la primera y tercer letra son cuadrados perfectos
(o tienen raíz cuadrada exacta) y son positivos y el segundo término es el
doble producto de sus raíces cuadradas.
—Ejemplos:
CUARTO CASO: DIFERENCIA DE CUADRADOS
—Se le llama diferencia de cuadrados al binomio conformado por dos
términos a los que se les puede sacar raíz cuadrada exacta.
—Al estudiar los productos notables teníamos que:
—En donde el resultado es una diferencia de cuadrados, para este capítulo
es el caso contrario:
—Donde siempre la diferencia de cuadrados es igual al producto de la
suma por la diferencia de sus bases.
—Pasos:
—Se extrae la raíz cuadrada de ambos términos.
—Se multiplica la suma por la diferencia de estas cantidades (el segundo
termino del binomio negativo es la raíz del termino del binomio que es
negativo).
—Ejemplos:







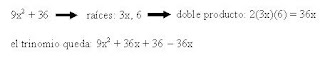
Comentarios
Publicar un comentario