Casos de factorización 3
Excelente día para todos anexo los últimos tres casos de factorización
para culminar con todos los casos, espero les sea de ayuda.
Octavo caso: Cubo perfecto de binomios
— Para
reconocerlo se deben tomar en cuenta los siguientes puntos:
— Debe
tener cuatro términos, y estar ordenado con respecto a una letra.
— Dos
de sus términos, el 1º (a) y el 4º (b), deben poseer raíz cúbica exacta.
— El
segundo término debe ser igual al triple producto del cuadrado de la raíz
cúbica del primer término por la raíz cúbica del cuarto termino [3(a)2(b)].
— El
tercer término debe ser igual al triple producto de la raíz cúbica del primer término
por el cuadrado la raíz cúbica del cuarto termino [3(a) (b)].
— El
segundo y el cuarto termino deben tener el mismo signo y puede ser positivo o
negativo, el primer y tercer término siempre son positivos (si el primer y
tercer término son negativos realizar factor común con el factor -1).
— Si
todos los términos son positivos el resultado es el cubo de la suma de dos
cantidades (a + b), si hay términos negativos el resultado es el cubo de la
diferencia de dos cantidades (a – b).
— Ejemplos:
Noveno caso: Suma o
diferencia de cubos perfectos
— Pero
en la división exacta el dividendo es igual al divisor multiplicado por el
cociente, efectuándolo nos queda:
— De
donde se deducen las siguientes reglas:
— La suma
de dos cubos perfectos se descompone en dos factores, el primero es la suma de
sus raíces cúbicas, y el segundo se compone del cuadrado de la primera raíz
menos el producto de ambas raíces más el cuadrado de la segunda raíz.
— La
diferencia de dos cubos perfectos se descompone en dos factores, el primero es
la diferencia de sus raíces cúbicas, y el segundo se compone del cuadrado de la
primera raíz más el producto de ambas raíces más el cuadrado de la segunda
raíz.
— Ejemplo
explicativo:
Décimo caso: Suma o
diferencia de dos potencias iguales
— Pero
en la división exacta el dividendo es igual al divisor multiplicado por el
cociente, al despejarlo nos queda:
— Y
esto es válido para cualquier diferencia de dos potencias iguales ya sean
impares o pares.
— Que es
válido para cualquier suma de dos potencias iguales impares únicamente
(con pares no funciona).
— Que es
válido para cualquier diferencia de dos potencias iguales pares únicamente (con
impares no funciona).
— Pasos:
— Clasificar
la expresión en positiva o negativa, y en par o impar (si son positivas y pares
no se pueden realizar por este método).
— Se
sacan las raíces de cada término.
— Se
coloca el primer factor el cual es un binomio cuyo primer término es la raíz
del primer término dado y el segundo término es la raíz del segundo término
dado.
— El
signo del primer factor (binomio) será el mismo que tiene la expresión dada.
— Se
crea el segundo factor (un factor polinomio) en el cual existirá un número de
términos igual al exponente de la expresión dada (los siguientes pasos son solo
para el segundo factor).
— En
cada término se multiplicara el término de la izquierda por el término de la
derecha de la expresión dada
— En
el primer término del factor polinomio el factor de la izquierda tendrá un
exponente igual a “n – 1”, y el factor derecho tendrá un exponente de cero.
— Para
los exponentes de los siguientes términos, en el caso del factor de la
izquierda irán disminuyendo en una unidad, y los del término de la derecha irán
aumentando también en una unidad (si se suman los exponentes de los dos
términos siempre será igual a n-1).
— Si
el binomio es negativo todos los términos del polinomio son positivos, si el
binomio es positivo impar los signos del
polinomio se alternarán (+ ó –) comenzando por el “+”.
— Cuando
en el polinomio, el exponente del término de la derecha sea igual a n-1 damos
por terminada la respuesta.
— Ejemplos
explicativos:
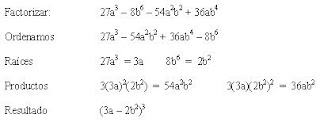











Comentarios
Publicar un comentario